Sémantická analýza textů (2)

V tomto článku se zaměříme na způsoby porovnávání dvou dokumentů a podíváme se na problémy, které přináší reprezentace dokumentů pomocí vektorů slov.

V předchozím dílu seriálu jsme definovali tzv. vector space model a ukázali si na příkladu, jak ve vektorovém prostoru reprezentovat libovolný textový dokument z dané kolekce dokumentů (korpusu). Nyní se zaměříme na to, jak lze této reprezentace využít pro fulltextové vyhledávání.

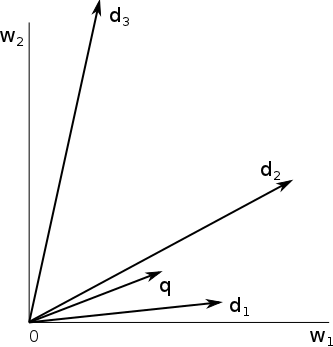
Jakmile dokážeme do konkrétního vektorového prostoru zobrazit dokument, dokážeme do stejného prostoru zobrazit i libovolný fulltextový dotaz, neboť i na něj lze nahlížet jako na množinu slov. Jak tedy nyní porovnat dva dokumenty, případně dotaz a dokument? Nejrelevantnější dokument pro dotaz je takový, jehož vektor leží nejblíže vektoru dotazu (zde považujeme za jediný zdroj informace pouze náš vektorový prostor, v reálných vyhledávačích se výsledky řadí podle celé řady dalších kritérií). Pokud se omezíme pouze na dvourozměrný prostor, lze situaci snadno graficky znázornit:

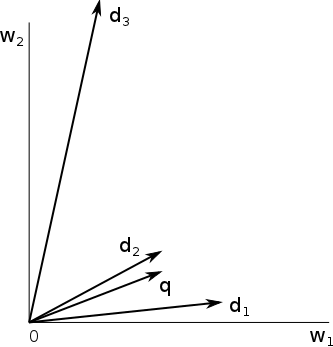
Obrázek zachycuje dvourozměrný vektorový prostor slov w 1 a w 2, do kterého jsou zobrazeny dokumenty d 1, d 2, d 3 a dotaz q. Je zde vidět, že nejblíže dotazu q z hlediska euklidovské vzdálenosti (vzdálenost koncových bodů šipek) leží dokument d 2. Co se ale stane, jestliže vezmeme dokument d 2 a všechna jeho slova zduplikujeme? Pokud neuvažujeme binární reprezentaci popsanou v předchozím dílu, ale např. TF nebo TF-IDF reprezentaci, vektor dokumentu se prodlouží na dvojnásobnou velikost a situace tedy bude vypadat následovně:

Vzdálenost dokumentu d 2 od dotazu q se zvětší natolik, že se nejbližším dokumentem dotazu stane d 1 , i když se d 2 významově nijak nezměnil. Abychom se takovému nežádoucímu jevu vyhnuli můžeme velikost všech vektorů normalizovat, anebo lépe, místo euklidovské vzdálenosti měřit úhel mezi vektory. Intuitivně, čím větší úhel dva vektory svírají, tím jsou od sebe vzdálenější. Často používanou metrikou, která reflektuje tento požadavek je cosinová míra.

Jakmile máme definovanou vzdálenost mezi vektory, můžeme mezi nimi začít vyhledávat. Přestože se úloha nalezení nejbližšího dokumentu dotazu může zdát snadná, je tomu naopak. Pokud už dokument reprezentujeme pomocí vektoru reálných čísel, většinou není možné použít pro vyhledávání jednoduché struktury jako je reverzní index. Jestliže chceme dosáhnout sublineární složitosti vyhledávání (tedy neporovnávat dotaz se všemi dokumenty v databázi), je třeba použít složitějších struktur, jakými jsou např. R-Tree nebo M-tree. Velice však záleží na rozmístění dat v prostoru a počtu dimenzí. Nedá se říci, která struktura je obecně nejlepší.

Jedním z největších problémů reprezentace objektů pomocí vektorů vysoké dimenze (každé dimenzi v našem modelu odpovídá právě jedno slovo, proto je počet dimenzí v řádu statisíců) je takzvané „prokletí dimenzionality“. S tím, jak roste počet dimenzí, exponenciálně roste velikost prostoru, ve kterém se vektory nacházejí a většina objemu se začíná hromadit na samých okrajích. Při velkých dimenzích jsou důsledkem toho všechny dokumenty od sebe vzdáleny téměř stejně daleko.

Mezi další problémy reprezentace dokumentů vektory slov patří synonymie a homonymie, které jsou pro přirozené jazyky tolik typické. Pokud bychom v našem prostoru porovnávali např. dokument obsahující pouze dvě slova „tenisové rakety“ s dotazem „sportovní potřeby“, vzdálenost bude obrovská, a to i přesto, že tématicky jsou si velice blízko. Bude tomu tak proto, že dotaz a dokument nemají žádná společná slova. Naopak dotaz „vesmírné rakety“ bude našemu dokumentu určitě blíže, přestože nemá tematicky s tenisem ani sportem nic společného.

Na nejjednodušší způsoby, jak snížit počet dimenzí se podíváme v příštím dílu. Problém víceznačnosti a synonymie bude diskutován později.