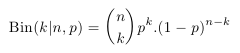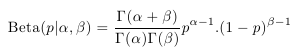Sémantická analýza textů (6)

Tématem dnešního dílu seriálu je další metoda pravděpodobnostní sémantické analýzy textů, která se jmenuje Latentní Dirichletova alokace.  Jedná se o jednu z nejpokročilejších, a v současnosti zřejmě vůbec nejpoužívanější, metodu identifikace skrytých témat v textech.

V předchozím dílu seriálu jsme si představili metodou nazvanou Pravděpodobnostní latentní sémantická analýza a seznámili se s jejími hlavními výhodami a nevýhodami. Mezi její největší nedostatky patří tendence k přeučování a především nemožnost odvození témat nových dokumentů, které nebyly součástí trénovací množiny. Oba tyto problémy řeší metoda nazvaná Latentní Dirichletova Alokace (LDA).

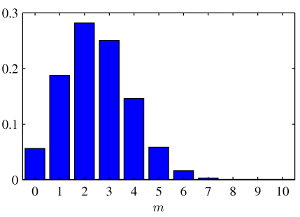
Dříve než se pustíme do vysvětlení principu LDA si připomeňme dvě základní rozdělení pravděpodobnosti, která budeme pro pochopení LDA potřebovat. Prvním z nich je binomické rozdělení, které popisuje četnost výskytu náhodného jevu v n nezávislých pokusech. Příkladem použití může být n hodů „cinknutou“ mincí, která má pravděpodobnost 1/4 pro padnutí panny a 3/4 pro orla, a zajímá nás, jaká je pravděpodobnost, že padne k-krát panna. Rozdělení pravděpodobnosti je dáno následujícím vztahem: 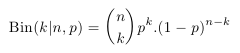kde p^k vyjadřuje pravděpodobnost, že k-krát padne panna, (1-p) ^ (n-k) pravděpodobnost, že (n-k)-krát padne orel a kombinační číslo n nad k zajišťuje normalizaci tak, aby byl součet přes všechny hodnoty k roven jedné. Histogram rozdělení pro hodnoty n = 10 a p = 1/4 je pro názornost zobrazen na následujícím obrázku:

Situace se začne komplikovat v případě, že neznáme pravděpodobnost p. Pokud však o ní máme částečnou představu, můžeme její hodnotu modelovat pomocí dalšího rozdělení pravděpodobnosti. Vhodným rozdělením pravděpodobnosti pro modelování parametru p binomického rozdělení je takzvané beta rozdělení, které je definováno následovně:

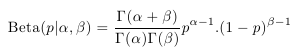Rozdělení má dva parametry – alfa a beta, podle jejichž volby se zásadně mění podoba rozdělení, jak je vidět na následujících grafech:

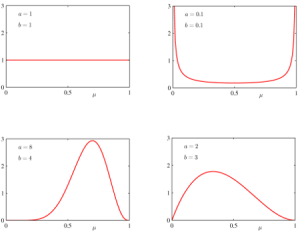Obrázek vlevo nahoře zobrazuje případ, kde alfa = beta = 1, ve kterém jsou všechny hodnoty p stejně pravděpodobné. Oba obrázky dole představují případy, kde jsou alfa i beta  > 1 a existuje nějaká hodnota p, která je nejpravděpodobnější. Z hlediska LDA je však nejzajímavější graf vpravo nahoře, kde platí alfa = beta = 0,1. V tomto případě je nejpravděpodobnější, že p je buď 0 nebo 1, ale obě možnosti mají pravděpodobnost stejnou. Pokud se vrátíme k našemu příkladu s mincí, znamená to, že víme, že mince je s největší pravděpodobností „cinknutá“, jen nevíme na kterou stranu.

Tato dvě rozdělení představují základ LDA. Jediné, co ještě budeme potřebovat je zobecnění ze dvou rozměrů (panna, orel) do n rozměrů. Vícerozměrná varianta binomického rozdělení se nazývá multinomické rozdělení a vícerozměrná varianta beta rozdělení Dirichletovo rozdělení. Rozdíl je v tom, že už neházíme mincí, ale n-stěnnou kostkou a zajímá nás např. jaká je pravděpodobnost, že ze dvaceti hodů padne 3x jednička, 8x šestka a 9x pětka. Pro detailnější vhled do zmiňovaných rozdělení pravděpodobnosti lze doporučit libovolnou učebnici statistiky, pro pochopení LDA by nám však měly stačit výše popsané základy.

Nyní se již můžeme pustit do vysvětlení principu samotné Latentní Dirichletovy alokace. Stejně jako u pLSA předpokládejme, že v naší množině dokumentů chceme identifikovat k témat. Budeme postupovat stejným způsobem jako u pLSA. Tedy postupně vyjádříme pravděpodobnost generování naší kolekce dokumentů, a poté budeme hledat takové parametry, které tuto pravděpodobnost maximalizují. Pomocí těchto parametrů již bude možné vyjádřit vše, co potřebujeme, tedy především vektor témat pro každý dokument a rozdělení pravděpodobnosti slov pro každé téma. Tomuto postupu se říká generativní model a pro LDA vypadá následovně:

1. Pro každý dokument i z kolekce všech dokumentů vyber parametry multinomického rozdělení theta(i) z Dirichletova rozdělení s parametry alfa. Obě rozdělení mají k dimenzí – tedy tolik, kolik témat chceme identifikovat. Alfa je vektor k reálných čísel menších než 1, která jsou společná pro všechny dokumenty a jedná se o tzv. hyperparametr LDA modelu. Pro každý dokument tedy vybereme pravděpodobnosti pro všechna z k témat. Díky volbě parametrů Dirichletova rozdělení menších než 1 bude zajištěno, že s největší pravděpodobností bude mít pouze několik málo témat nezanedbatelnou pravděpodobnost, neříkáme však, která to budou. To odpovídá skutečnosti, kde dokument většinou pojednává pouze o několika málo tématech.
2. Pro každou pozici slova j v dokumentu i vyber z Dirichletova rozdělení s parametry theta(i) téma z(i,j). Pro každou slovní pozici v dokumentu si tedy hodíme k-stěnnou kostkou, jejíž pravděpodobnosti jsou dány parametry theta(i) a přiřadíme pozici příslušné téma.
3. Pro každou pozici (i, j) vyber slovo w(i, j)  z multinomického rozdělení phi(z(i,j)). Multinomické rozdělení phi slov pro témata je globální a podobně jako theta má parametry generované z Dirichletova rozdělení, tentokrát s parametrem beta.

Pro nalezení parametrů LDA, a tudíž i požadovaných vektorů témat pro dokumenty, je stejně jako u pLSA třeba maximalizovat pravděpodobnost modelu pro poskytnutá trénovací data. Na rozdíl od pLSA by však bylo použití Expectation-Maximization algoritmu příliš složité, proto se pro inferenci v LDA využívají aproximativní metody. Mezi nejčastěji používané patří variační metody a Gibbsovo vzorkování.

Oproti pLSA má LDA řadu výhod, především řeší jeho nejpalčivější problémy. Díky tomu, že má LDA fixní počet parametrů, jejichž počet s přibývajícími dokumenty neroste, nedochází k přeučování a dosahuje tak výrazně vyšší kvality. Hlavní výhoda ale spočívá v tom, že lze díky generativnímu přístupu odhadovat témata i pro nové dokumenty, které nebyly přítomny v trénovací množině. Z těchto důvodů se pLSA téměř nepoužívá a v praktických aplikacích převažuje LDA.

Jak pLSA, tak LDA má řadu rozšíření a modifikací, těmi se ale v tomto seriálu zabývat nebudeme. V příštím, a současně posledním dílu, si ukážeme příklady toho, jak lze sémantické analýzy textů využít v praktických aplikacích nejen ve fulltextových vyhledávačích.