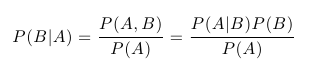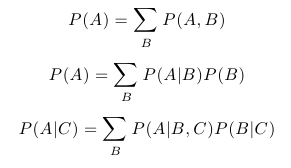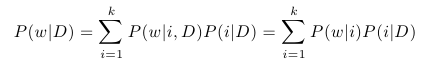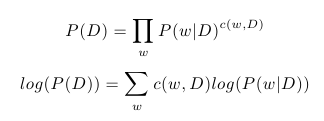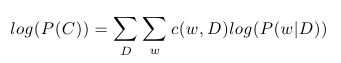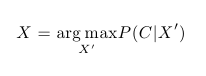V dnešním dílu seriálu si představíme další automatickou metodu pro identifikaci témat dokumentů. Tato metoda je založená na pravděpodobnostním přístupu a nese název Probabilistic Latent Semantic Analysis.
V předchozím článku jsme si představili první z algoritmů pro redukci dimenzionality, který dokáže automaticky identifikovat množinu témat a jejich přiřazení ke slovům a dokumentům. Jednalo se o metodu s názvem Latentní sémantická analýza, založenou na aplikaci lineární algebry, konkrétně tzv. Singular Value Decomposition. Metoda nazvaná Probabilistic Latent Semantic Analysis (dále pLSA), řeší stejný problém, ale na rozdíl od LSA je založena na pravděpodobnosti a statistice.
Pro lepší porozumění pLSA si nejprve shrňme základy pravděpodobnostního počtu. Pravděpodobností jevu A nazýváme číslo P(A) = a/n, kde a je počet příznivých jevů a n je počet všech všech možných jevů univerza. Např. pokud házíme šestistěnnou kostkou a označíme A jev, kdy nám padlo sudé číslo, je P(A) = 3/6 = 1/2, neboť sudá čísla na kostce jsou 3 a všech čísel dohromady je 6. Pokud uvažujeme dva náhodné jevy, které jsou na sobě nezávislé, pravděpodobnost, že nastanou oba současně je dána součinem obou pravděpodobností. Pro příklad, pokud B označíme jev, kdy nám na kostce padla 6, pravděpodobnost, že nám při dvou hodech nejprve padlo sudé číslo a při druhém hodu 6 je dána P(A, B) = P(A)*P(B) = 1/2 * 1/6 = 1/12. Pokud nás však zajímá pravděpodobnost, že při jednom hodu kostkou padlo sudé číslo a je to zároveň 6, pak už se o nezávislé jevy nejedná a P(A, B) = 1/6.
Dalším velice důležitým pojmem pravděpodobnostního počtu je podmíněná pravděpodobnost. Jak sám název napovídá, jedná se o pravděpodobnost jevu při daných omezujících podmínkách. Např. by nás mohlo zajímat, jaká je pravděpodobnost, že nám na kostce padla 6 za předpokladu (podmínce), že nám padlo sudé číslo. Podmíněná pravděpodobnost jevu B za předpokladu A se zapisuje P(B | A) a v našem příkladu s kostkou intuitivně platí P(B | A) = 1/3. Obecně je podmíněná pravděpodobnost definována jako:
A skutečně platí P(B | A) = P(A,B) / P(A) = (1/6)/(1/2) = 1/3. Mezi další snadno odvoditelná pravidla, která budeme potřebovat, patří následující:
Nyní už se můžeme pustit do vysvětlení principu pLSA. Předpokládejme, že v naší množině dokumentů chceme identifikovat k témat. Dále předpokládejme, že s každým tématem i je spojeno rozdělení pravděpodobnosti přes všechna slova w, která se množině dokumentů vyskytují. Jedná se tedy o funkci, která pro dané téma i přiřazuje každému slovu jeho pravděpodobnost, díky které dokážeme vyjádřit P(w | i) pro libovolné w a i. Tato funkce je samozřejmě předem neznámá. Dále předpokládejme, že je s každým dokumentem D spojena podmíněná pravděpodobnost P(i | D), která udává pravděpodobnost výskytu tématu i v dokumentu D. Tyto pravděpodobnosti jsou také předem neznámé. Pokud bychom tyto neznámé parametry znali, mohli bychom vyjádřit pravděpodobnost výskytu slova w v dokumentu D pomocí posledního ze zmíněných pravidel následovně:
Pravděpodobnost P(w | i, D) můžeme zjednodušit na P(w | i) díky tomu, že chceme mít rozdělení pravděpodobnosti slov pro témata globální, nezávislé na dokumentu.
Model pLSA předpokládá, že každé slovo dokumentu je generováno z právě jednoho tématu a slova v dokumentu jsou navzájem nezávislá. Pravděpodobnost dokumentu tedy můžeme vyjádřit jako:
kde, c(w, D) značí počet výskytů slova w v dokumentu D. Díky tomu, že je logaritmus monotónní funkce, můžeme celý výraz zjednodušit zlogaritmováním. Jestliže označíme C množinu všech dokumentů v naší kolekci, může vyjádřit logaritmus pravděpodobnosti celé kolekce jako:
Nyní známe způsob, jak vyjádřit pravděpodobnost naší kolekce dokumentů, ale neznáme parametry P(i | D) a P(w | i). Ty naopak chceme určit. Všechny tyto neznámé označme X. Standardním způsobem jejich identifikace je hledání takových parametrů X, které maximalizují pravděpodobnost P(C | X), případně log(P(C | X)). Tato metoda je založená na maximalizaci věrohodnosti dat. Řešením je tedy optimalizační úloha:
Tuto úlohu lze vyřešit např. algoritmem Expectation-Maximization. Jakmile známe pravděpodobnosti P(i | D) pro libovolný dokument D a téma i, můžeme každý dokument z kolekce reprezentovat vektorem témat, podobným LSA, kde každá složka určuje pravděpodobnost výskytu tématu v dokumentu.
Podobnost dvou dokumentů, případně dotazu a dokumentu, lze měřit stejným způsobem jako u LSA. Vhodnější je však použít některou z podobnostních funkcí, navržených přímo pro porovnávání pravděpodobnostních rozdělení. Mezi nejčastěji používané patří KL-divergence nebo její symetrická varianta Hellingerova vzdálenost.
Oproti LSA má pLSA výhodu v solidním matematickém základu. Výsledky dosažené s pLSA jsou skutečně výrazně lepší než u LSA. Velkým nedostatkem je však nemožnost predikce vektoru témat u nových dokumentů, které nebyly obsaženy v trénovací kolekci C. Další nevýhodou je tendence k přeučování, neboť s rostoucím počtem dokumentů v trénovací kolekci roste i počet parametrů, které je třeba odhadnout. Oba tyto nedostatky řeší metoda nazvaná Latent Dirichlet Allocation, o které bude následující díl seriálu.