Jak vysvětlujeme složité modely (třeba relevanci)

Vyvinuli jsme interní nástroj pro srozumitelné vysvětlení složitějších modelů strojového učení a nasadili ho mimo jiné i na náš model pro výpočet relevance. Nyní dokážeme jednoduššeji interpretovat složité SEO metriky pro interní potřeby. V tomto teoretickém článku vysvětlíme princip našeho nástroje inspirovaného [Strumbelj.2010] a [Strumbelj.2014] právě na příkladu modelu relevance.

Za výběrem podobného dokumentu pro hledaný výraz (tzv. relevance) se skrývá složitý algoritmus strojového učení (tzv. model), a proto občas není jasné, proč se hodnocení některých dokumentů dramaticky změnilo. Abychom zjistili příčiny takových změn, musíme rozumět vlastnímu modelu, což v případě neuronových sítí a náhodných lesů není triviální úkol. Algoritmicky je vysvětlení modelu celkem nenáročné. Ovšem časová složitost je velký problém. Vstup jakéhokoliv modelu je několik příznaků (features), které jsou pro pohodlí většinou číselné. Pokud bychom na stránce hodnotili pouze 2 věci, např.

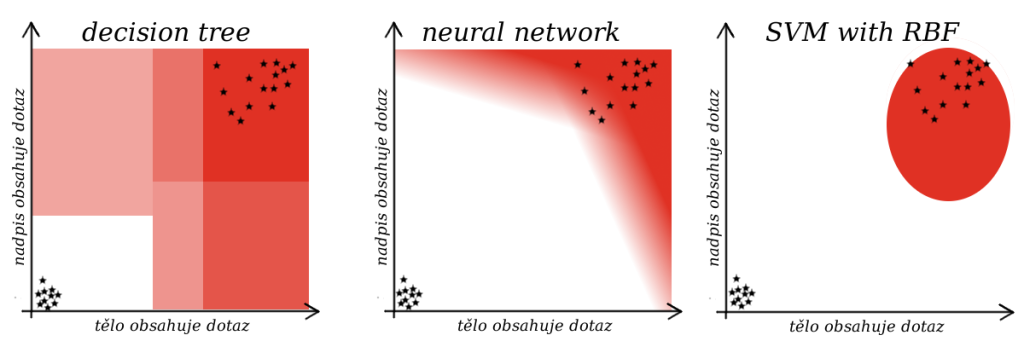
1. jak moc nadpis stránky obsahuje slova z dotazu (od 0.0 do 1.0)

2. jak moc se opakují slova z dotazu v těle stránky (od 0.0 do 1.0)

pak si můžeme celý český internet představit na jedné ploše, která bude různá pro každý dotaz. Vezměme například dotaz “krásný výlet”, na jehož ploše se budou v nějakém místě tísnit vedle sebe weby o turistice a kolem nuly bude vše ostatní. Umístění na ploše je konstantní a je dáno obsahem stránky. Relevanci si pak můžeme představit jako barvu plochy, která se mění od (dejme tomu) červené, která bude kolem turistických webů, až do bílé kolem nulových hodnot. Toto vybarvování provádí právě náš model.

Pro vysvětlení, jak si dokument vede pro daný dotaz, musíme vzít bod reprezentujcí náš dokument a zašoupat s ním v jeho blízkém okolí a pozorovat jak se mění jeho barva. Ovšem abychom dostali vypovídající výsledek, je potřeba zkusit pohyb paprskovitě ve všech směrech, protože nevíme, kde se barvy mění. Může se stát, že náš model započítává hodnocení těla dokumentu, až když nalezne shodu v nadpisu stránky. Pak šoupáním v oblasti příznaku pro tělo textu bychom vysvětlili, že na něm vůbec nezáleží, což není pravda! Takovému modelu se technicky říká, že není aditivní. Aditivní modely lze totiž vysvětlit aritmetickou kombinací příznaků = není tam žádná hranice (můžeme si představit jako funkci IF).

Jak tedy správně hýbat bodem v prostoru, aniž bychom zkusili všechny směry a vzdálenosti, kterých je v podstatě nekonečně? Odpovědí je metoda Monte Carlo, která v podstatě říká, že nemusíme zkoumat celý prostor, ale stačí se dívat na náhodná místa v prostoru, z čehož dostaneme dostatečně dobrou představu o prostoru. Samozřejmě čím déle vydržíme, tím více se blížíme tomu, že jsme prozkoumali celý prostor.

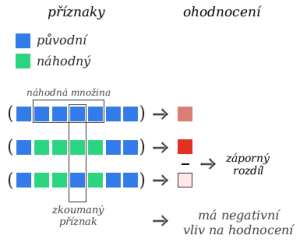
Jak tedy napočítávání příspěvků příznaků funguje? V naší implementaci zkoumáme příznaky jeden po druhém (nikdy více naráz). Pokaždé ke zkoumanému příznaku vybereme pár dalších a podíváme se na rozdíl barev, když změníme hodnoty všech vybraných příznaků a všech bez zkoumaného příznaku. Rozdílu těchto dvou barev nazýváme příspěvek zkoumaného příznaku.

Výběrem nějaké množiny příznaků simulujeme hýbnutí v prostoru nějakým “šikmým” směrem. Celý postup vlastně odhaduje průměrnou barvu v okolí a porovnání s hodnotou v našem bodě.

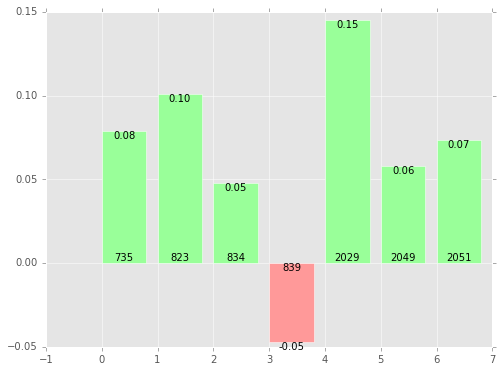
Využití je pak celkem přímočaré. Zvolíme jeden příklad – nějaký dotaz a nějaký dokument, a podíváme se, které příznaky mají pozitivní a negativní vliv na jeho hodnocení. Surovým výstupem jsou hodnoty v intervalu <-1.0, ₊1.0>. Na obrázku 1.3. vidíme reálný příklad z našeho hodnotícího modelu, které příznaky (zde kódované pořadovými čísly) mají jaký vliv na dobré hodnocení dokumentu.

Pokud by příznak 839 byl například počet mezer v nadpisu, tak můžeme zavolat majiteli dokumentu, že mu nejspíš při psaní ujel mezerník a po takhle jednoduché opravě by se opět vrátil na výsluní první stránky vyhledávače.